Полезность прибыли — это не сама прибыль

Приветствую всех в своем первом посте!👋

Планирую опубликовать здесь несколько своих размышлений на тему личных финансов и инвестиционного планирования. Они достаточно общие и не связаны с какими-то конкретными тикерами. Надеюсь это соответствует тематике клуба! Также надеюсь, что для кого-то это будет полезной информацией для размышления, а другие укажут мне на мои ошибки, и мы вместе приблизимся к истине🤝

Полезность прибыли — это не сама прибыль

Что вы выберете: получить $1,000,000 с вероятностью 10% или $100,000 с вероятностью 90%? Такую дилемму ставит автор книги "Просто делай! Делай просто!" Оскар Хартманн. В книге утверждается, что рациональный человек должен выбрать первый вариант. Действительно, с точки зрения теории вероятности математическое ожидание прибыли в первом варианте больше:

$1,000,000 * 10 % = $100,000 против $100,000 * 90 % = $90,000.

Но наверняка вас не покидает ощущение, что, интуитивно хочется выбрать именно второй вариант. Оказывается, у второго варианта, действительно, есть строгое математическое объяснение.

Деньги нам нужны не сами по себе. Они цены тем, что мы можем купить за них какие-либо товары и услуги. Именно в этом состоит полезность денег. Допустим вы мечтаете купить iPhone за 100,000 руб. Осуществив мечту, вы будете счастливы. Это означает, что затраченная сумма денег увеличила ваше счастье на какую-то величину. В следующим году выходит новая модель, и вы решаете купить и ее. Второй iPhone не принесет вам такого же счастья, как первый, то есть полезность следующих 100,000 рублей будет ниже, чем первых. Таких примеров можно приводить сколько угодно, и всегда вы будете замечать, что первое "что угодно" является гораздо ценнее, чем последующее "что угодно".

Давайте разберем еще пример из другой области. Например, вы переехали в мегаполис и желаете купить там собственную квартиру. Вы долго копили деньги (или долго платили ипотеку) и вот квартира стоимостью 5 млн. рублей ваша! Вы счастливы? Конечно! Дальше ваш достаток растет, и вы задумываетесь о покупке более просторной квартиры, да и еще желательно поближе к работе, но она стоит 10 млн. рублей. Вы опять копите 5 млн. и покупаете квартиру. Во сколько раз счастливее вы будете после этой покупки, если сравнить это с покупкой первой квартиры? Уж точно не в 2 раза, как следует из цены!

Отношения с деньгами на интуитивном уровне примерно такие же. Первый заработанный миллион делает вас значительно счастливее, но каждый последующий не прибавляет такого же счастья. Интуитивно вы понимаете, что все базовые потребности вы закрыли своим первым миллионом, а для дорогих предметов роскоши второго миллиона уже недостаточно, и надо, как минимум, уже миллионов десять...

Функция полезности денег для каждого человека индивидуальная и ее довольно тяжело определить (в следующей статье будет описан способ как оценить ее хотя бы примерно), поэтому чаще всего считают ее логарифмической:

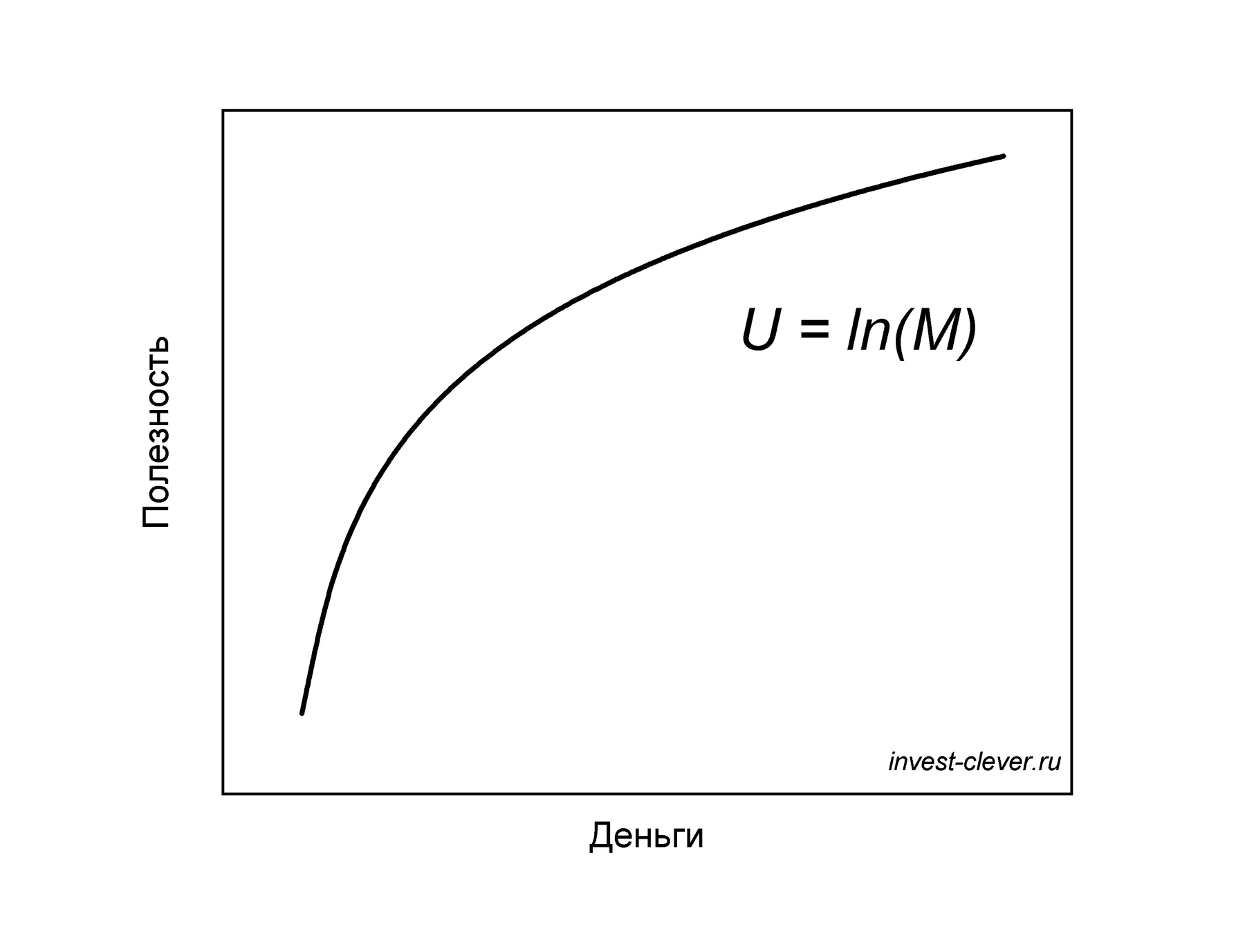
Свойство вогнутости функции показывает как раз то, что каждый последующий рубль способен обеспечить все меньшую полезность. Это так называемое свойство убывающей предельной полезности.

Теперь вернемся к дилемме из книги "Просто делай! Делай просто!". Во-первых, определим сумму имеющихся у человека накоплений, так как любую инвестиционную перспективу нужно рассматривать не в вакууме, а относительно своего капитала. Пусть оптимистично совокупный капитал человека будет $100,000. Перспектива получить $1,000,000 означает увеличение капитала в 11 раз, а $100,000 — в 2 раза. Применим логарифмическую формулу функции полезности (для любой другой вогнутой функции результат будет аналогичным):

U ($1,000,000) = ln(11) = 2.4

U ($100,000) = ln(2) = 0.7

В первом варианте мы получаем полезность 2.4 с вероятность 10 %, то есть математическое ожидание полезности равно 0.24. Во втором случае полезность 0.7 достигается в 90 % случаев, значит, мат. ожидание равно 0.63. Ожидаемая полезность второго варианта почти в 3 раза выше!

Интуитивно это можно объяснить так: для человека среднего достатка $100,000 — большая сумма, которая может резко изменить его жизнь. Миллион долларов, конечно, может изменить ее гораздо серьезнее, но не в 10 раз.

Как видите, многое зависит от вашего начального капитала. Давайте рассмотрим случай, когда рассматриваемые суммы маленькие. Например, пусть это будет:

Вариант 1: $100 с вероятностью 10 %.

Вариант 2: $10 с вероятностью 90 %.

Поскольку, это небольшие суммы относительно вашего капитала, то, скорее всего, вы скажите: "ОК, раз математика так говорит, я выбираю первый вариант. Ничего страшного, если я не заработаю сегодня $100." Полезность этих двух вариантов будет такая:

U ($100) = ln(1.001) = 0.001

U ($10) = ln(1.0001) = 0.0001

Далее рассчитываем математическое ожидание:

M1 = 0.001 10 % = 0.0001

M2 = 0.0001 90 % = 0.00009

И действительно, первый вариант оказывается выгоднее. Это, потому что в области малых значений функция полезности почти прямая, а по мере увеличения сумм она все больше загибается. Кстати, если для вас $1,000,000 — небольшая сумма от вашего капитала, то выбирать, конечно, нужно именно первый вариант, как и сделал автор книги.

Выводы

• Полезность денег — не равно количеству денег! Таким образом пословица "счастье не в деньгах, а в их количестве" не соответствует действительности😀 Правильнее было бы сказать: "Счастье не в деньгах, а в той пользе, которую они приносят".
  

• Все индивидуально. Форма функции полезности зависит от вашего характера, но она всегда остается вогнутой, что называется правилом убывающей предельной полезности. Также многое будет зависеть от вашего изначального капитала — состоятельный человек рискнет $100,000, а человек среднего достатка — вряд ли.
  

• Учитывайте что "Полезность прибыли — это не сама прибыль" и не берите на себя излишнего инвестиционного риска, но и не слишком избегайте его!
  
  

© Invest-Clever.ru